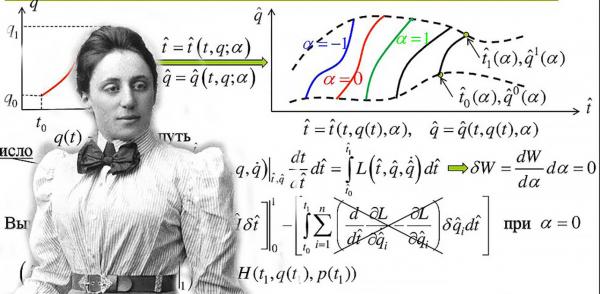
Мы продолжаем вспоминать вместе с вами научные достижения 1918 года и оценивать их с позиций дня сегодняшнего. В прошлый раз мы говорили о физике, а в этот раз предлагаем небольшой экскурс в историю математики.
Как известно, Нобель по своим причинам оставил математиков «за бортом» своей знаменитой премии. Но это совсем не значит, что история этой науки в ХХ веке не имела выдающихся результатов. И один из них был получен как раз в 1918 году. Этому результату не так давно посвятил свою лекцию известный физик и науковед Алексей Левин.
Произошло это в Гёттингенском университете, который стараниями работавших там профессоров Феликса Клейна и Давида Гильберта в начале прошлого века превратился в своего рода «математическую мекку». Причем, даже сражения Первой мировой войны не сумели помешать этому.
Ситуация для математиков, на самом деле, вполне естественная – катаклизмы окружающего мира не имеют для них значения в сравнении с научными задачами. Известный российский математик Дмитрий Меньшов, к примеру, делился со студентами своими воспоминаниями о молодости: «А в 1917 году произошло событие, перевернувшее нашу жизнь [речь шла о членах Московского математического общества], мы занялись теорией функциональных тригонометрических рядов». Это было для него главным событием того года. Равно как и его коллеги в Германии больше внимания обращали на свою работу, чем на сводки с фронтов. Несмотря на то, что привычный мир довоенной Европы рушился на глазах.
В июльские дни 1918 года внештатная сотрудница математического отделения философского факультета Эмми Нётер представила его преподавателям (в числе которых – уже упоминавшиеся Гильберт и Клейн) свою работу, позже названную теоремой Нётер. Эмми приехала в Гёттинген в 1916 году, а до того на протяжении семи лет работала в математическом институте Университета Эрлангена (где читал лекции ее отец – математик Макс Нётер). Работала бесплатно, поскольку в то время для женщины было практически невозможно занять академическую должность. К слову, попытки Гильберта сделать Нётер приват-доцентом Гёттингенского университета тоже провалились из-за сопротивления профессуры. И потому в 1918 году дальнейшее представление ее работы взял на себя профессор Феликс Клейн.
В Гёттингене Нётер изначально занималась теорией непрерывных групп. Но вскоре Гильберт поручил ей работу над совсем другой темой. Ранее он немало времени посвятил изучению работ Эйнштейна, которые еще только оформлялись в знаменитую теорию относительности. И даже сумел доказать ее своим, отличным от эйнштейновского, способом. А попутно пришел к выводу, что в общей теории относительности незыблемость закона сохранения энергии оказывается под вопросом.
– Это тот самый принцип эквивалентности Эйнштейна, – подчеркнул Левин. – Если наблюдатель падает в гравитационном поле с тем ускорением, которое создает в этой точке поле, то он будет чувствовать себя в невесомости, а не действие гравитации.
Возникает вопрос: если в любой точке гравитацию можно «обнулить», то как говорить о сохранении энергии гравитационного поля. К поискам ответа на этот вопрос Гильберт и подключил Эмми Нётер, поскольку понимал, что для решения этой задачи надо работать с некими инвариантами (а Нётер несколько лет занималась работой именно в схожем направлении).
Она взялась за эту работу и уже через несколько месяцев получила впечатляющий результат, смысл которого в то время понимала, пожалуй, только она и еще два-три коллеги по Гёттингенскому университету.
Он был оформлен в виде теоремы, которую она и представила в своем докладе в июле 1918 года. Эта теорема связала закон сохранения с каждой дифференцируемой симметрией физической системы. Американские физики Леон М. Ледерман и Кристофер Т. Хилл написали в своей книге «Симметрия и прекрасная Вселенная» о том, что теорема Нётер является «безусловно, одной из самых важных математических теорем, используемых в современной физике, возможно, она находится на одном уровне с теоремой Пифагора».
– Это был абсолютно фундаментальный результат, который показал, что законы сохранения ключевых физических величин связаны с симметриями и вытекают из симметрии, – вторит им в своей оценке Алексей Левин.
Второй результат теоремы заключается в математическом доказательстве того, что в рамках теории общей относительности в классическом виде не работают. И если можно говорить о сохранении энергии, то только в каком-то необычном смысле слова.
Хотя результаты Нётер и были понятны в то время единицам (Эйнштейн, к слову, оценил возможности ее теоремы), постепенно она завоевывала себе «место под солнцем» в мужском мире немецкой математики. В 1919 году Гильберт добился-таки для нее должности приват-доцента. А три года спустя Нётер получила письмо от прусского министра науки, искусства и народного образования, в котором говорилось о присвоении ей титула профессора с ограниченными внутренними административными правами и функциями.
К тому времени, Нётер уже переключилась на другую задачу, с которой ее имя и связывают в первую очередь. Известный американский математик Натан Джекобсон по этому поводу писал:
«Развитие общей алгебры, которая стала одним из самых примечательных новшеств математики двадцатого века, в значительной степени заслуга Нётер – её опубликованных статей, её лекций, её личного влияния на современников».
Единственным ее вкладом в физику так и осталась эта работа и сформулированная теорема. Но зато физики, начиная с 1950-х годов, регулярно опираются на эту теорему в своих исследованиях. Особенно те, что занимались разработкой квантовых теорий поля. Что интересно, в прошлый раз, когда мы говорили про достижения собственно физиков, то вспоминали Нобелевскую премию Планка как раз за создание квантовой теории как таковой.
– Физики осознали, что с помощью теоремы Нётер можно разбираться в очень тонких математических аспектах практически любых полевых теорий, – заключил лектор.
И все это благодаря тому, что у нее был чрезвычайно общий подход к решению поставленной Гильбертом задачи. А вообще, сама эта история служит хорошей иллюстрацией роли, которую играет математика для естествознания. Остается лишь пожалеть, что Альфред Нобель почему-то отказался эту роль признавать.
Наталья Тимакова
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии