Весенний сезон научно-популярных мероприятий (в рамках проекта «Лекторий plus+») в Информационном центре по атомной энергетике (ИЦАЭ) Новосибирска открылся лекцией, посвященной, наверное, самой известной математической константе – числу π. Рассказывала о нем заместитель директора Математического центра новосибирского Академгородка, профессор, д.ф.-м.н. Дарья Лыткина.
Тема была выбрана не случайно: 14 марта (день проведения лекции) математики всего мира отмечают День числа π. В 1988 году американский физик Ларри Шоу заметил, что в американской системе записи дат (месяц / число) дата 14 марта — 3/14 совпадает с числом π и предложил учредить к этой дате математический праздник. Идея пришлась по вкусу, а неофициальный статус праздника открыл широкие возможности для творчества на тему, как лучше его отметить. На «родине» праздника уже традиционно устраивают карнавальное шествие: первым идет Ларри с табличкой, на которой нарисована тройка, следом – участник с табличкой с цифрой «один», затем – с «четверкой» и так далее. Благо, количество цифр после запятой у этой константы считается бесконечным, а значит, и число участников парада – неограниченно.
 Надо сказать, что часть математиков (в основном из стран, где принято записывать даты в ином формате – сначала день, потом месяц) предложила альтернативную дату – 22 июля, указывая на то, что дробь 22/7 точнее приближает число π, чем 3,14. Однако пока большинство их коллег продолжает праздновать в марте. В этот день читают хвалебные речи в честь числа π, его роли в жизни человечества, рисуют антиутопические картины мира без π, пекут и едят «пи-рог» («Pi pie») с изображением греческой буквы «пи» или с первыми цифрами самого числа, пьют напитки и играют в игры, начинающиеся на «пи», решают головоломки и загадки, водят хороводы вокруг предметов, связанных с этим числом.
Надо сказать, что часть математиков (в основном из стран, где принято записывать даты в ином формате – сначала день, потом месяц) предложила альтернативную дату – 22 июля, указывая на то, что дробь 22/7 точнее приближает число π, чем 3,14. Однако пока большинство их коллег продолжает праздновать в марте. В этот день читают хвалебные речи в честь числа π, его роли в жизни человечества, рисуют антиутопические картины мира без π, пекут и едят «пи-рог» («Pi pie») с изображением греческой буквы «пи» или с первыми цифрами самого числа, пьют напитки и играют в игры, начинающиеся на «пи», решают головоломки и загадки, водят хороводы вокруг предметов, связанных с этим числом.
Тем временем, в 2006 году Конгресс США включил этот день в официальный список американских праздников (правда, без объявления выходного дня), а спустя несколько лет решением ЮНЕСКО за ним закрепился международный статус.
Ну а в этом году у числа π еще и свой юбилей – 314 лет с того времени, как его придумали. В 1706 году британский математик Уильям Джонс впервые предложил греческую букву π для обозначения отношения длины окружности к её диаметру (поскольку эта буква начальная в греческих словах περιφέρεια — окружность, периферия и περίμετρος — периметр).
Рассказав историю математического праздника, Дарья Викторовна перешла к самому числу, благо, с ним связано немало фактов и даже заблуждений, интересных не только математикам.
Во-первых, это очень древняя математическая постоянная. Еще в третьем тысячелетии до нашей эры в древней Греции, Египте, Вавилоне люди обнаружили, что длина веревки, обернутой вокруг колеса, примерно в три раза больше диаметра этого колеса. Причем такая пропорция соблюдалась для любых окружностей. Важность этой величины осознали уже тогда, прежде всего, для инженерных расчетов. С тех времен начался поиск точного значения отношения длины окружности к ее диаметру.
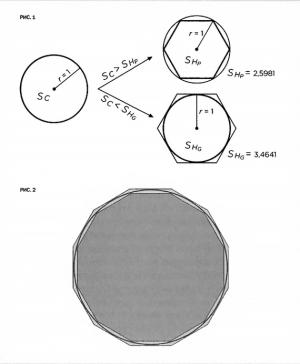 Внес свой вклад в ее расчеты известный древнегреческий математик, физик и инженер Архимед. В те времена перед античными математиками встала проблема – как вычислять площадь криволинейных фигур, кругов, овалов и т.п. Частично решить ее удалось с помощью метода исчерпывания (впервые его применил Евклид, а Архимед взял на вооружение и усовершенствовал). Чтобы его использовать, надо вписать один многоугольник в окружность, а другой описать вокруг нее, тем самым зажав ее между ними. Площадь многоугольников вычислять греки умели, значение площади окружности располагалось где-то в интервале между большим и меньшим многоугольником. Причем, чем больше было сторон у многоугольников, тем меньше был интервал, а следовательно – точнее был результат вычисления площади окружности. И первым эту идею выдвинул как раз Архимед, для начала заменив шестиугольник (который использовали до него) на двенадцатиугольник.
Внес свой вклад в ее расчеты известный древнегреческий математик, физик и инженер Архимед. В те времена перед античными математиками встала проблема – как вычислять площадь криволинейных фигур, кругов, овалов и т.п. Частично решить ее удалось с помощью метода исчерпывания (впервые его применил Евклид, а Архимед взял на вооружение и усовершенствовал). Чтобы его использовать, надо вписать один многоугольник в окружность, а другой описать вокруг нее, тем самым зажав ее между ними. Площадь многоугольников вычислять греки умели, значение площади окружности располагалось где-то в интервале между большим и меньшим многоугольником. Причем, чем больше было сторон у многоугольников, тем меньше был интервал, а следовательно – точнее был результат вычисления площади окружности. И первым эту идею выдвинул как раз Архимед, для начала заменив шестиугольник (который использовали до него) на двенадцатиугольник.
Далее он продолжил увеличивать число сторон и дошел до фигуры с 96 углами. В итоге, была сформулирована т.н. «аксиома Архимеда» о том, что можно найти настолько близкий к площади криволинейной фигуры многоугольник, насколько пожелаешь, но при этом точного результата все равно не достигнешь. Ограничением, по сути, служили цели вычислений, для хозяйственных нужд можно было округлять сильнее, а для научных трактатов – вычислять с максимально возможной точностью. Сам Архимед рассчитал, что соотношение длины окружности и диаметра равно 3( 10)⁄71, он также доказал, что площадь круга равна числу этого соотношения, умноженному на квадрат радиуса круга.
На многие века этой точности людям хватало, но все изменилось вместе с появлением математического анализа, если точнее – с началом вычислений сумм бесконечных рядов. В итоге, число цифр после запятой в числе π быстро стало расти. Сейчас благодаря огромным вычислительным способностям современных компьютеров, число π известно с точностью до 10 триллионов знаков после запятой. Существует даже версия, что оно (в силу своей бесконечности) включает в себя все возможные комбинации цифр, например, номера мобильных телефонов всех людей на планете или оцифрованный текст всех художественных произведений. Но математики подчеркивают – это предположение доказать на сегодня невозможно.
Что известно точно, так это то, что число π является иррациональным и трансцедентальным. Первое означает, что его значение не может быть точно выражено в виде дроби, где числитель и знаменатель являются целыми числами. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. А вторая характеристика говорит нам о том, что оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа π, то доказательство его трансцендентности положило конец попыткам построить квадратуру круга, длившимся не одну тысяч лет.
Люди, далекие от математики, склонны думать, что эта постоянная является неким научным казусом, интересным только ученой публике. Но это не верно. Как уже говорилось, его используют в решении различных инженерных задач, с его помощью определяют углы на окружности. Число π можно встретить во многих разделах физики (имеющих и вполне себе прикладное значение), от теории колебаний до квантовых задач. А не так давно ему нашлось место и в географии: оказалось, что совокупное соотношение длины русла всех рек на планете к совокупному расстоянию от их истока до устья тоже равно этому числу. И никто не может предсказать, где еще «всплывет» это иррациональное, трансцедентальное и такое загадочное число.
Сергей Исаев
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии

